流行病学的数学原理 1：Survival, hazard, and Incidence

在流行病学课本中，关于累计发病率（Cumulative incidence, CI）和发病密度(incidence rate, IR)之间有如下关系：

$$ CI = 1 - e^{\sum_i-IR_i \times \Delta T_i} $$

在 Modern Epidemiology (Edition 3) 中，简要说明了该公式离散形式的推导过程（P43）。在此通过积分的方法来证明该公式的连续形式，即:

$$ CI_{t_1,t_2} = 1 - \exp\left[-\int_{t_1}^{t_2}IR(t)dt\right] $$

假设一个理想的 close cohort，没有失访和竞争结局，所有个体都随访至结局发生，在此 cohort 上，可以定义函数 $N(t)$，表示在时间 $t$ 时，尚未发生结局的个体数。函数如下图所示：

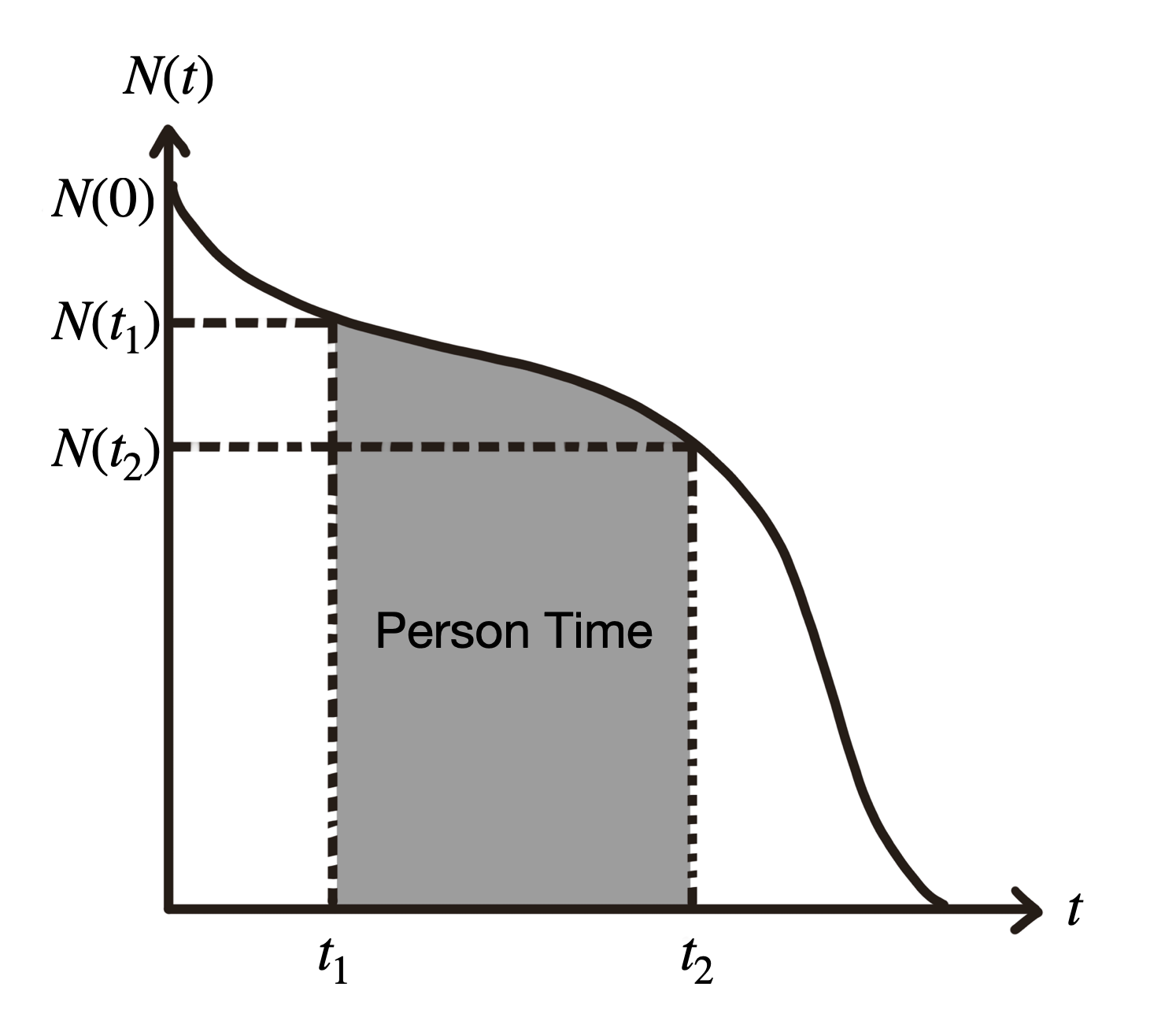
根据 CR 和 IR 的定义，有： $$ \begin{aligned} IR_{t_1,t_2} &= \frac{N(t_1)-N(t_2)}{\int_{t_1}^{t_2}N(t)dt} \\ \\ CR_{t_1,t_2} &= \frac{N(t_1) - N(t_2)}{N(t_1)} \end{aligned} $$

这里的 $IR_{t_1,t_2}$ 为一段时间内的发病密度，而如果考虑一个瞬时的发病密度，有：$IR(t) = \frac{-dN(t)}{N(t)dt}$。值得注意的是，这个瞬时的发病密度在生存分析中有重要的意义，即某一时刻的 hazard rate （$h(t)$）。将 $IR(t)$ 的公式带入原式右侧，有：

$$ \begin{aligned} &1 - \exp\left[-\int_{t_1}^{t_2}IR(t)dt\right] \\ =&1 - \exp\left[-\int_{t_1}^{t_2}\frac{-dN(t)}{N(t)dt}dt\right] \\ =&1 - \exp\left[\int_{t_1}^{t_2}\frac{dN(t)}{N(t)}\right] \\ =&1 - \exp\left[\ln\left(\frac{N(t_2)}{N(t_1)}\right)\right] \\ =&1 - \frac{N(t_2)}{N(t_1)} \\ =&CR_{t_1,t_2} \end{aligned} $$

由此，得到了 CI 和 IR 之间的关系。在实际使用中，该公式可以进行简化，如当 IR 保持稳定，即 $IR(t)$ 可以近似为常函数时，该公式可以化简为：$CI = 1 - \exp\left[-IR*\Delta t\right]$。进一步，如果 CI 本身较小（<0.1），则数学上有如下近似：$1-x \approx\exp(-x)$，则有：$CI \approx IR*\Delta t$。直觉上理解，当发病率较低时，因为确诊患者所损失的后续随访人时相对于总的人时微不足道，因此只需要在发病密度上乘以相应的时间间隔即可大概估计累计发病率。

上文提到，某一时点的发病密度其实就是生存分析中的风险率（hazard rate），即 $h(t) = \frac{-dN(t)}{N(t)dt}$。这里借助了一个 close cohort 的剩余人数随随访时间变化的函数 $N(t)$。而在生存分析中，更常见的做法是定义一个随机变量 $T, T\geq 0$，表示某一事件的发生时间。对于这个随机变量，有累计分布函数（CDF）和概率密度函数（PDF）：

$$ \begin{aligned} f(t) &= \frac{dF(t)}{dt} \\ F(t) &= P(T\leq t) = \int_{0}^{t}f(x)dx \end{aligned} $$

这里 CDF $F(t)$ 表示在时间 $t$ 之前发生事件的概率，因此生存函数定义为 $S(t) = 1 - F(t)$，表示在时间 $t$ 之前没有发生事件的概率。而 hazard rate $h(t)$ 则定义为：

$$ \begin{aligned} h(t) &\overset{\Delta}{=} \lim_{\Delta t \to 0}\frac{P(t\leq T < t+\Delta t|T\geq t)}{\Delta t} \\ &= \lim_{\Delta t \to 0}\frac{P(t\leq T < t+\Delta t)}{P(T\geq t)\Delta t} \\ &= \frac{f(t)dt}{S(t)dt} \\ &= \frac{f(t)}{S(t)} \\ &= -\frac{d\ln S(t)}{dt} \end{aligned} $$

最后一步反向推导更简单：$-\frac{d\ln S(t)}{dt} = -\frac{d\ln(1-F(t))}{dt}=-\frac{d\ln(1-F(t))}{d(1-F(t))}\frac{d(1-F(t))}{t}=\frac{f(t)}{1-F(t)}$。当然接下来可以对 $h(t)$ 进行积分，得到累积风险 $H(t) = \int_0^th(x)dx=-\ln[S(t)]$。

部分参数模型中会假设生存时间 $T$ 的分布。最简单的模型是指数分布，即 $f(t) = \lambda e^{-\lambda t}$，其中 $\lambda$ 为分布参数。对应的生存函数为 $S(t) = e^{-\lambda t}$，$h(t) = \lambda$。这个模型的特点是风险是恒定的，即 hazard rate 不随时间变化。更复杂的模型会假设生存时间服从 Weibull 分布，在此不再赘述。关于生存函数、风险函数这一部分内容可以参考斯坦福大学的讲义。